3 应用案例
本章将介绍DS-PAW的各种应用实例,具体包括:如何计算磁矩、如何计算反铁磁材料等;用户通过以下应用教程,可以更深入了解DS-PAW软件的使用。
3.1 \(O\) 原子的磁矩计算
本节将以单个氧原子体系为例来介绍磁性体系的计算。
\(O\) 原子自洽计算之文件准备
由于本次计算的是单个氧原子的磁矩,因此并不需要进行结构弛豫计算,直接从自洽计算开始,准备参数文件 scf.in 和结构文件 structure.as , scf.in 如下:
task = scf
sys.symmetry = false
sys.structure = structure.as
sys.spin = collinear
cal.smearing = 1
cal.sigma = 0.01
cal.kpoints = [1, 1, 1]
本次计算的输入文件中以下几个参数需重点关注:
sys.symmetry:DS-PAW可以通过对称性来减少程序的计算量,但同时可能会带来能量简并等不合理的结果,本次计算关闭对称性;sys.spin:指定体系的磁性为 collinear 即 共线自旋 ;cal.kpoints:对于没有周期性的维度, K点可设置为1;
structure.as 文件参考如下:
Total number of atoms 1 Lattice 7.50000000 0.00000000 0.00000000 0.00000000 8.00000000 0.00000000 0.00000000 0.00000000 8.90000000 Cartesian O 0.00000000 0.00000000 0.00000000
结构文件使用笛卡尔坐标,因此第七行中坐标类型为 Cartesian ;为了使结构也尽量地减少对称性,将晶格修改为 [7.5,8,8.9] 格子。
run程序运行
准备好输入文件之后,将 scf.in 和 structure.as 文件上传到安装了DS-PAW的环境上,运行 DS-PAW scf.in 命令。
analysis计算结果分析
根据上述的输入文件,计算完成之后将会得到 DS-PAW.log 、 scf.h5 等输出文件。
使用HDFView软件打开 scf.h5 文件,Eigenvalue 部分数据如下:

在 scf.h5 的 Eigenvalue - Spin - Occupation 部分可得向上自旋的电子占据数为4,向下自旋的电子占据数为2,从 MagInfo 部分可得总磁矩为 2μB ,同时在 DS-PAW.log 中也可读取体系的总磁矩为 2μB 。
3.2 \(NiO\) 体系的反铁磁计算
本节将以NiO体系为例介绍如何设置计算反铁磁计算。
\(NiO\) 体系自洽计算
本次案例省略了结构弛豫过程,用户重现此案例时需先进行结构弛豫计算。准备参数文件 scf.in 和结构文件 structure.as , scf.in 如下:
task = scf
sys.structure = structure.as
sys.spin = collinear
cal.smearing = 4
cal.kpoints = [8, 8, 8]
cal.cutoff = 650
本次计算的输入文件中以下几个参数需要重点关注:
cal.smearing:本次计算中采用 四面体加布洛赫 的方法,当使用该方法时sigma将强制被设置为 0 ;sys.spin:指定体系磁性, NiO 为反铁磁材料因此设置磁性为collinear;cal.cutoff:设置平面波的截断为 650 eV ;
structure.as 文件参考如下:
Total number of atoms
4
Lattice
4.16840000 2.08420000 2.08420000
2.08420000 4.16840000 2.08420000
2.08420000 2.08420000 4.16840000
Cartesian Mag
Ni 1.04210000 1.04210000 1.04210000 2.0
Ni 5.21050000 5.21050000 5.21050000 -2.0
O 3.12630000 3.12630000 3.12630000 0
O 7.29470000 7.29470000 7.29470000 0
设置磁矩需在结构文件的第七行的 Cartesian 后加上 Mag 标签,在原子坐标所在行设置每个原子的磁矩,由于需要体现反铁磁(整个体系不显示磁矩,单个原子有磁矩),此例选取了4个原子的晶胞,设置4个Ni原子的磁矩分别为 2、-2、0、0 。
备注
Mag 标签可设置体系中各原子的磁矩。线性自旋计算中添加每个原子的总磁矩即可;自旋轨道耦合计算中需添加x, y, z方向上的磁矩,添加标签为 Mag_x , Mag_y, Mag_z,在对应的原子坐标后添加三个方向上磁矩即可。以NiO体系为例,若进行自旋轨道耦合计算,磁矩设置应如下:
Total number of atoms
4
Lattice
4.16840000 2.08420000 2.08420000
2.08420000 4.16840000 2.08420000
2.08420000 2.08420000 4.16840000
Cartesian Mag_x Mag_y Mag_z
Ni 1.04210000 1.04210000 1.04210000 0.0 0.0 2.0
Ni 5.21050000 5.21050000 5.21050000 0.0 0.0 -2.0
O 3.12630000 3.12630000 3.12630000 0.0 0.0 0.0
O 7.29470000 7.29470000 7.29470000 0.0 0.0 0.0
run程序运行
准备好输入文件之后,将 scf.in 和 structure.as 文件上传到安装了DS-PAW的环境上,运行 DS-PAW scf.in 命令。
analysis自洽计算结果分析
根据上述的输入文件,计算完成之后将会得到 DS-PAW.log 、 scf.h5 等输出文件。从 DS-PAW.log 中可读取自洽完成之后总磁矩为 1e-8μB ,几乎为0。
\(NiO\) 体系态密度计算
之后准备进行态密度计算,准备参数文件 pdos.in 结构文件 structure.as 、自洽计算所得的电荷密度文件 rho.bin ,此时 pdos.in 如下:
task = dos
sys.structure = structure.as
sys.spin = collinear
cal.iniCharge = ./rho.bin
cal.smearing = 4
cal.kpoints = [16, 16, 16]
cal.cutoff = 650
dos.range = [-20, 20]
dos.resolution = 0.05
dos.project = true
pdos.in 输入参数介绍:
dos.range:表示能量计算区间为 -20 到 20 eV;dos.resolution:表示在能量计算区间内打点的间隔精度;dos.project:控制态密度的投影计算,本次计算打开了态密度的投影。
run程序运行
将新建的 pdos.in 文件上传至服务器,运行 DS-PAW pdos.in 命令。
dos态密度计算结果分析
根据上述的输入文件,计算完成之后将会得到 DS-PAW.log 、 dos.h5 等输出文件。使用 辅助工具使用教程 中相应脚本对 dos.h5 文件进行数据处理,分析第2个Ni原子的t2g和eg轨道,可得如下所示态密度分布图,此为不加U值的情况:

\(NiO\) 态密度
\(NiO\) 体系DFT+U的态密度计算
NiO体系DFT+U的态密度计算的计算流程与上节NiO体系的态密度计算流程一致,不同之处在于需在自洽和态密度的计算中都加入DFT+U相关参数,需增加的输入参数如下所示:
#correction related
corr.dftu=true
corr.dftuForm = 1
corr.dftuElements =[Ni]
corr.dftuOrbital=[d]
corr.dftuU = [8]
corr.dftuJ = [0.95]
本次计算的输入文件中以下几个参数需要重点关注:
corr.dftu设置是否打开DFT+U的开关,本例子中设置为true;corr.dftuForm设置DFT+U方法,1对应DFT+U+J 方法 (Liechtenstein’s formulation);corr.dftuElements设置需要加U的元素,本例中为Ni;corr.dftuOrbital设置需要加U的轨道,本例中设置为d轨道;corr.dftuU设置具体的U值,本例中设置为8;corr.dftuJ设置具体的J值,本例中设置为0.95;
自洽和态密度计算完成之后,分析第2个Ni原子在进行DFT+U计算之后t2g和eg轨道态密度分布,得到的分布图如下所示:

\(NiO\) 态密度( DFT+U )
备注
DFT+U可以设置多个元素对应轨道的U值,例如设置Ni的d轨道加U值为8,J值为0.95;O的p轨道加U值为1,J值为0,此时设置如下:corr.dftuElements =[Ni,O] corr.dftuOrbital=[d,p] corr.dftuU = [8,1] corr.dftuJ = [0.95,0]。
DFT+U默认使用方法为 DFT+U(Dudarev’s formulation),对应参数 corr.dftuForm = 2,使用该方法时 J 值强制为0,因此在该情况下设置J值无效。
3.3 \(AuAl\) slab模型功函数计算
本节将以 \(AuAl\) slab模型为例介绍如何进行功函数计算。
\(AuAl\) slab模型自洽计算之文件准备
本次案例省略了结构弛豫过程,用户重现此案例时需先进行结构弛豫计算。准备参数文件 scf.in 和结构文件 structure.as , scf.in 如下:
task = scf
sys.structure = structure.as
sys.spin = collinear
cal.smearing = 4
cal.kpoints = [8, 8, 1]
cal.cutoff = 530
io.potential=true
potential.type = hartree
#correction related
corr.dipol = true
corr.dipolDirection = c
本次计算的输入文件中以下几个参数需要重点关注:
io.potential为自洽中计算势函数的开关;potential.type控制势函数保存的类型,计算功函数的时候需要静电势的数据,这里我们设置potential.type = hartree;corr.dipol为偶极修正的开关;本例中设置为true;corr.dipolDirection本例中设置偶极修正的方向为晶格矢量的c方向。
structure.as 文件参考如下:
Total number of atoms
8
Lattice
4.06384898 0.00000000 0.00000000
0.00000000 4.06384898 0.00000000
0.00000000 0.00000000 20.00000000
Cartesian
Au 1.01596223 1.01596223 0.00000000
Au 3.04788672 3.04788672 0.00000000
Au 3.04788672 1.01596224 2.03914999
Au 1.01596224 3.04788672 2.03914999
Al 1.01596224 1.01596224 4.07109999
Al 3.04788673 3.04788673 4.07109999
Al 3.04788673 1.01596224 6.09585000
Al 1.01596224 3.04788673 6.09585000
结构参考如下图:

run程序运行
准备好输入文件之后,将 scf.in 和 structure.as 文件上传到安装了DS-PAW的环境上,运行 DS-PAW scf.in 命令。
workfunction功函数数据分析
根据上述的输入文件,计算完成之后将会得到 DS-PAW.log 、 scf.h5 等输出文件。对 scf.h5 文件进行数据处理可得功函数。
可使用 python 脚本分析 scf.h5 文件,将三维势函数进行面内平均,具体操作见 辅助工具使用教程 部分。处理得到的真空方向势函数曲线如下所示:

\(AuAl\) 一维势函数图
通过势函数的面内平均图,可得Au和Al的真空电势分别为5.5 ev 和 4.6 eV
从 scf.h5 中可读取费米能级为 0.113 eV
根据公式 \(w=-e \phi-E_F\) 可得 \(AuAl\) slab模型中,Au的功函数为 5.387 eV,Al的功函数为 4.487 eV。文献参考值[1] :Au的功函数在 5.10-5.47 eV区间,Al的功函数在 4.06-4.26 eV区间。
3.4 \(Ru-N4\) 电催化氮还原反应计算
本节将展示如何使用DS-PAW模拟一个电催化还原氮气反应(Electrocatalytic nitrogen reduction reaction, eNRR)。该反应以碳基负载过渡金属Ru单原子为催化剂,使用DS-PAW对电催化氮气分子的吸附及还原过程进行模拟。
在电化学界面反应过程中,由于电化学反应界面通常与恒定电极电势的外电极相连,为确保电子的化学势与外电极的电势达到平衡,即电子的巨正则系综(grand canonical ensemble),实际体系中会存在电子的流入与流出过程。传统的第一性原理计算通常是在正则系综下,即在电荷守恒的条件下展开的,因此它并不能很好的描述电化学界面反应,我们将在电荷守恒的条件下展开的计算模型称为恒电荷模型(constant charge model,CCM)。
因恒电荷模型并不适于处理电化学界面问题,我们可采用在电子巨正则系综下展开第一性原理计算,这种计算方法又被称为固定电势方法(fixed potential method/constant potential method)。在此例中我们将利用固定电势计算的模型称为恒电势模型(constant potential model,CPM)。
Flow计算流程及输入文件
此例以碳基负载过渡金属Ru单原子为催化剂,使用DS-PAW对电催化氮气分子的吸附及还原过程进行模拟。模拟的反应为氮气分子在碳基负载Ru单原子上的吸附过程,反应的表达式可简写作: \((Ru-N_4) + N_2 = (Ru-N_4-N_2)\) ,在计算过程中使用了CCM_vacuum,CCM_water,CPM_water 三种不同的模型,整个计算流程可大致分为四步,步骤展开如下:
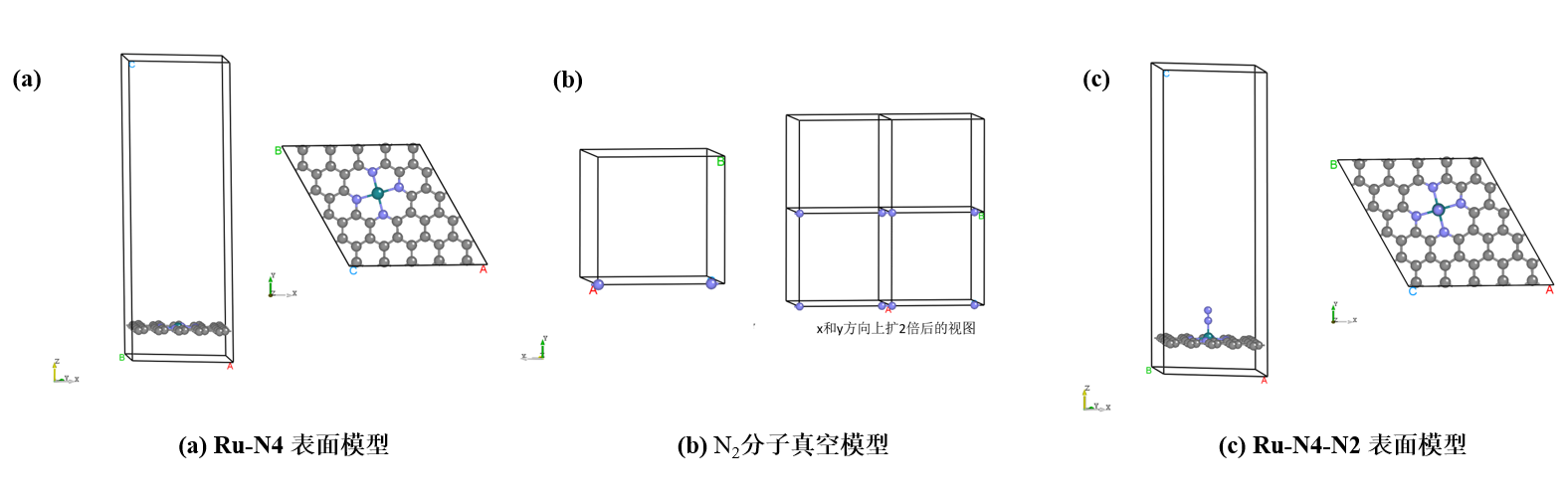
Build搭建模型
模型包括:(a) 碳基负载Ru原子模型 \((Ru-N_4)\) ,(b) \(N_2\) 单分子模型 , (c) 吸附了 \(N_2\) 分子的碳基负载Ru原子模型 \((Ru-N_4-N_2)\),模型图如下所示:
Relaxation结构弛豫
对搭建的结构进行结构弛豫,获得稳定结构,在DS-PAW中进行结构弛豫需要的核心参数:
relax.max = 200 #指定结构驰豫时最大的离子步步数
relax.freedom = atom #指定结构驰豫的自由度
relax.convergence = 0.02 #指定结构驰豫时原子受力的收敛判据
relax.methods = CG #指定结构驰豫的方法为共轭梯度法
Energy能量计算
在不同模型条件下进行能量计算,获得稳定构型对应能量,下面按不同模型分别进行介绍:
CCM_vacuum
常规的真空层下的scf计算,即可获得CCM_vacuum模型下的能量,下面列出了在DS-PAW中进行 单点能计算 需要设置的核心参数:
task = scf
#自洽计算相关
cal.methods = 1 #指定自洽电子部分优化的方法为BD(block Davidson)方法
cal.smearing = 1 #指定Gaussian smearing来设置每个波函数的部分占有数
cal.ksamping = G #指定生成布里渊区k点网格的方法
cal.kpoints = [2, 2, 1] #指定布里渊区k点网格取样大小
cal.cutoffFactor = 1.0 #指定平面波基矢的截断能参数cal.cutoff的系数
corr.VDW = true #指定引入范德瓦尔斯修正计算
corr.VDWType = D2G #指定DFT-D2 of Grimme方法进行范德瓦尔斯修正
CCM_water
在CCM模型下,也可以利用隐式溶剂化模型来考虑溶剂效应,这里我们以水溶液为例,列出利用DS-PAW在scf计算中引入 溶剂化模型 所需要设置的核心参数:
task = scf
#溶剂化模型相关
sys.sol = true #指定是否应用隐式溶剂化模型,true表示打开
sys.solEpsilon = 78.4 #指定溶剂介电常数,水的介电常数78.4
sys.solLambdaD = 3.04 #指定泊松玻尔兹曼方程中德拜长度,单位为Å
sys.solTAU = 0 #指定单位面积的有效界面张力的大小,单位eV/Å^2
io.boundCharge = false #指定是否输出溶剂束缚电荷密度文件,false表示关闭
CPM_water
在DS-PAW中用固定电势方法计算即可获得CPM模型下的能量。在新发布的2023A版本中进行固定电势计算必须引入溶剂化模型,这里列出了利用DS-PAW在隐式水溶液环境下进行 固定电势计算 的核心参数:
task = scf
#溶剂化模型相关
sys.sol = true #指定是否应用隐式溶剂化模型,true表示打开
sys.solEpsilon = 78.4 #指定溶剂介电常数,默认值为水的介电常数78.4
sys.solLambdaD = 3.04 #指定泊松玻尔兹曼方程中德拜长度,单位为Å
sys.solTAU = 0 #指定单位面积的有效界面张力的大小,单位eV/Å^2
io.boundCharge = false #指定是否输出溶剂束缚电荷密度文件,false表示关闭
#固定电势设置相关
sys.fixedP = true #指定是否开启固定电势计算,true表示打开
sys.fixedPConvergence = 0.01 #指定固定电势计算的收敛精度,前后两次自洽计算的delta_electron小于收敛精度,计算结束
sys.fixedPMaxIter = 60 #指定固定电势计算时最大迭代步数
sys.fixedPPotential = 0 #指定固定电势计算的目标电极电势值,默认以SHE为参考电极电势
sys.fixedPType = SHE #指定sys.fixedPPotential给出的电势值的电势类型,支持SHE(标准氢电极)和PZC(零电荷电位)
ReactionEnergy反应能计算
此例选取了3个不同的计算模型,首先介绍各模型下的吸附反应式:
CCM_vacuum
该模型下,吸附反应式可写作:
\((Ru-N4) + N2 (ideal gas) = (Ru-N4-N2)\)
我们定义 \({\Delta}E\) 为反应能,反应能的计算表达式为:
\({\Delta}E = E0(Ru-N4-N2) - E0(Ru-N4) - E0(N2)\)
其中,E0对应真空模型下体系的总能((sigma→0),该数值可从自洽计算所得的 scf.h5 或 system.json 文件中获取,查找关键字 “TotalEnergy0” 即可。
CCM_water
该模型下,吸附反应式可写作:
\((Ru-N4)(in water) + N2 (ideal gas) = (Ru-N4-N2) (in water)\)
\({\Delta}E = E0(Ru-N4-N2) - E0(Ru-N4) - E0(N2)\)
其中,E0对应水溶液浸润的模型下体系的总能((sigma→0),该数值可从自洽计算所得的 scf.h5 或 system.json 文件中获取,查找关键字 “TotalEnergy0” 即可。
CPM_water
该模型下模拟的反应过程为气相中的 \(N_2\) 在由水溶液浸润并与0V vs. SHE(标准氢电极)电极接触的催化剂表面的吸附过程, 此时吸附反应式有两种写法 ,为便于描述,我们 定义了以下物理量符号 :
\(ne0\) : 中性体系下的核电荷数
\(ne\) : 当体系电压为设定值(sys.fixedPPotential所设数值,此例对应 0 V)时体系的总电子数
\(dne\) : 当体系电压为设定值时,体系的带电量: \(dne = ne - ne0\)
\(\mu_e\) : 体系电子化学势,电势零点为溶液深处(即DFT计算得到的电荷密度最低点的电势值)
\({\Delta}e\) : 吸附态体系价电子数(eAB)与吸附基底和吸附分子总价电子数(eA+eB)的差值
\(\Omega0\) : grand total energy(sigma→0): 电子巨正则系综下的体系总能,其表达式为 : \(\Omega0 = E0-dne*\mu_e\)
此时,CPM_water模型下吸附反应式可参考如下写法:
方法一,在反应式中考虑 \({\Delta}e\) ,吸附反应式可写作:
\(Ru-N4 (0V vs. SHE) + N2(ideal gas) = Ru-N4-N2 (0V vs. SHE) - {\Delta}e\)
\({\Delta}E = E0(Ru-N4-N2) - {\Delta}e*\mu_e - E0(Ru-N4) - E0(N2)\)
其中,E0的数值可从自洽计算所得的 scf.h5 或 system.json 文件中获取,查找关键字 “TotalEnergy0” 即可。
\(ne\) 和 \(\mu_e\) 的数值可从自洽计算所得的 DS-PAW.log (或 scf.h5 或 system.json)文件中获取,最后一个LOOP下查找关键字 “Electron” 和 “Chemical Potential(electron) ” 即可。
方法二,考虑电子巨正则系综下的体系总能 \(\Omega0\)
由于固定电势计算是模拟的电子的巨正则系综,此时反应能计算式中的体系总能 \(E0\) 应当用 \(\Omega0\) 来代替。吸附反应式可写作:
\((Ru-N4) (0V vs. SHE) + N2(ideal gas) = (Ru-N4-N2) (0V vs. SHE)\)
\({\Delta}E = \Omega0(Ru-N4-N2) - \Omega0(Ru-N4) - \Omega0(N2)\)
其中,\(\Omega0\) 的数值可从自洽计算所得的 DS-PAW.log (或 scf.h5 或 system.json)文件中获取,最后一个LOOP下查找关键字 “Grand Total Energy” 即可。
由于(Ru-N4)与(Ru-N4-N2)的电势为0V vs. SHE,故对(Ru-N4)与(Ru-N4-N2)进行0V下的固定电势计算,从DS-PAW的相应输出文件提取数据,得到如下表格,能量单位为 eV:
system |
\(E0\) |
\(nE0\) |
\(ne\) |
\(dne\) |
\(\mu_e\) |
\(\Omega0\) |
|---|---|---|---|---|---|---|
N2 |
-545.9393 |
10 |
/ |
/ |
/ |
-545.9393 |
Ru-N4 |
-10572.2452 |
212 |
211.224 |
-0.776 |
-4.60223 |
-10575.81654 |
Ru-N4-N2 |
-11119.6117 |
222 |
221.229 |
-0.771 |
-4.60054 |
-11123.15868 |
表 1. CPM_water模型下固定电势计算数据
接下来将 表 1 的数据代入对应的表达式中进行计算:
方法一 在反应式中考虑 \({\Delta}e\) ,反应能计算过程如下:
\(Ru-N4 (0V vs. SHE) + N2(ideal gas) = Ru-N4-N2 (0V vs. SHE) - {\Delta}e\)
\({\Delta}E = E0(Ru-N4-N2) - {\Delta}e*\mu_e - E0(Ru-N4) - E0(N2)\)
\(= -11119.6117-(221.229-211.224-10)*(-4.600)-(-10572.2452)-(-545.9393)\)
\(= - 1.4042 eV\)
方法二 考虑电子巨正则系综下的体系总能 \(\Omega0\) ,反应能计算过程如下:
\((Ru-N4) (0V vs. SHE) + N2(ideal gas) = (Ru-N4-N2) (0V vs. SHE)\)
\({\Delta}E = \Omega0(Ru-N4-N2) - \Omega0(Ru-N4) - \Omega0(N2)\)
\(= -11123.1586-(-10575.8165)-(-545.9393)\)
\(= -1.4027 eV\)
通过两种方法计算所得的吸附能一致。 可见 用DS-PAW中定义的 \(\Omega0\) 即可很方便的计算固定电势下的反应能。
Run程序运行
准备好输入文件之后,将结构弛豫计算、能量计算、固定电势计算的 in 文件和 structure.as 结构文件上传到安装了DS-PAW的环境上,按照流程分多步运行 DS-PAW input.in 命令或提交作业脚本完成多次计算。
ReactionEnergy反应能数据分析
将表 1的数据分别代入 CCM_vacuum 、 CCM_water 、 CPM_water 模型的吸附反应式,计算三个模型下, eNRR前三步反应的反应能,结果如下 表 2 所示:
reaction/ \({\Delta}e\) (eV) |
CCM_vacuum |
CCM_water |
CPM_water |
|---|---|---|---|
\((Ru-N4) + N2 = (Ru-N4-N2)\) |
-1.3180 |
-1.3668 |
-1.4027 |
\((Ru-N4-N2) + 0.5H2 = (Ru-N4-N2-H)\) |
1.1355 |
1.0833 |
1.6511 |
\((Ru-N4-N2-H) +0.5H2 = (Ru-N4-N2-H2)\) |
-0.6833 |
-0.8030 |
-1.0305 |
表 2. 反应能数据表
最后将上述结果绘制成反应坐标曲线,效果如下 图 3 所示:

图 3. 反应坐标-反应能曲线